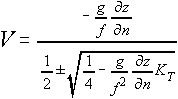
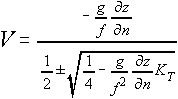
where:

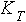 is the curvature term, being equal to
is the curvature term, being equal to 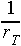
The gradient wind equation is a representation of the entire n equation of motion. There is a balance between all of the forces present in the n equation, those being the following:
The centrifugal force: 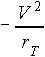

 The pressure gradient force:
The pressure gradient force: 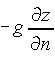

 The coriolis force:
The coriolis force: 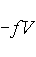
The gradient wind is very much like the geostrophic wind, in that it is a frictionless wind which allows for flow that is parallel to the height contours. The one difference between the geostrophic wind and the gradient wind is that the gradient wind includes the centrifugal force, thereby allowing curvature in the flow field. At first glance, this may seem to be simply an addition to the geostrophic wind equation, since the two flows are very similar to one another. For example, if the curvature is equal to zero, then geostrophic flow is obviously the result. However, the addition of the centrifugal force complicates the equation tremendously and creates several different solutions to the gradient wind equation.
In order to understand the possibilities, it is necessary to study the gradient wind equation more in depth. In the denominator of the gradient wind equation, there is a positive root and a negative root. Mathematically, there are only four possible solutions that can be computed. The table below illustrates these four possibilites:
| Sign of root | Sign of 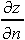 |
Positive 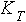 |
Negative 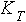 |
|---|---|---|---|
| Positive Root | Positive | Not Physical | Anomalous Low |
| Negative | Normal Low | Anomalous High | |
| Negative Root | Positive | Not Physical | Not Physical |
| Negative | Not Physical | Normal High |
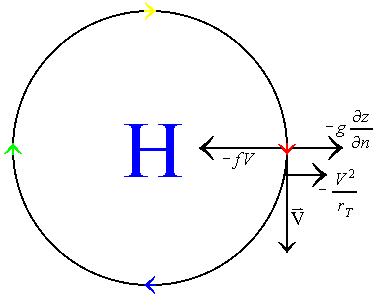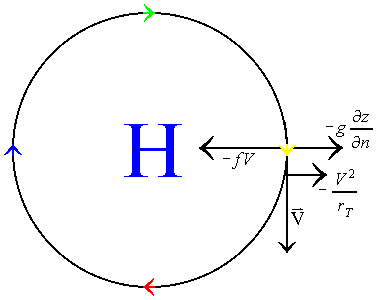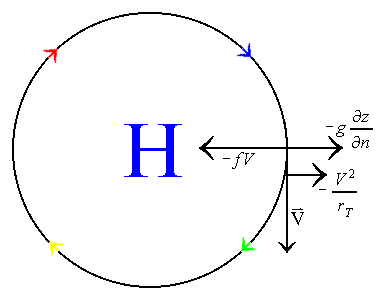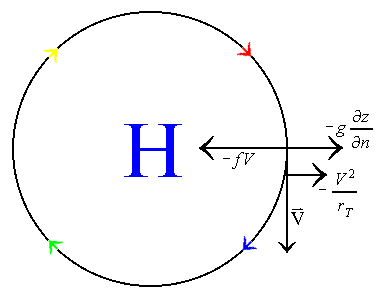
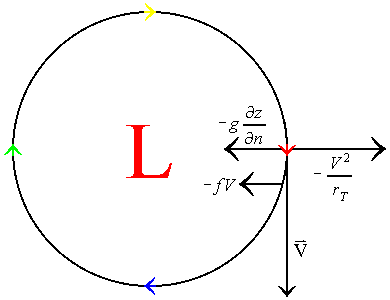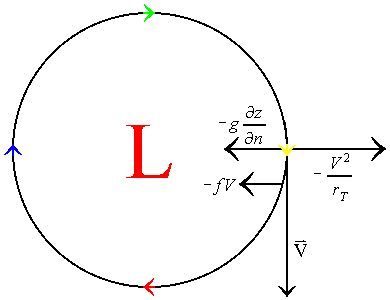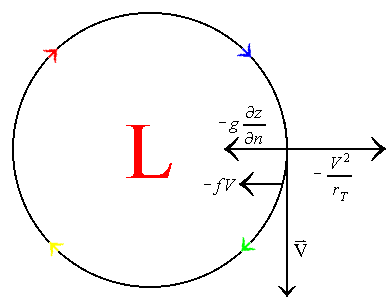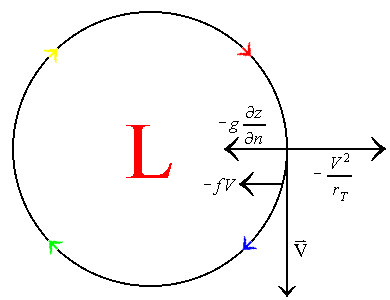
This table shows that the four possible physical solutions to the flow are gradient flows around normal high and low pressure systems, and anomalous high and low pressure systems. Normal, meaning that the flow around these systems is anti-cyclonic for high pressure systems and cyclonic for low pressure systems. Anomalous low pressure means that the flow is anti-cyclonic around the system. Yet, with anomalous high pressure, the flow is still anti-cyclonic, but the wind speed is much too high to represent a true high pressure system. The following illustrates each of these four possible gradient flows:
| Normal Low Pressure System | Normal High Pressure System |
|---|---|
 |
 |
| Anomalous Low Pressure System | Anomalous High Pressure System |
 |
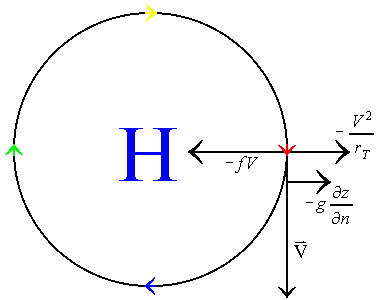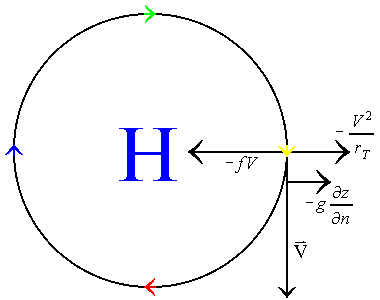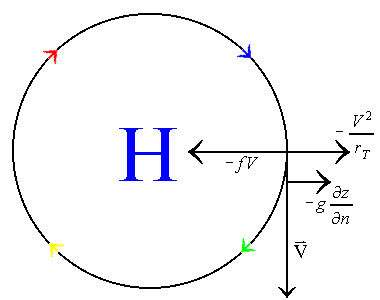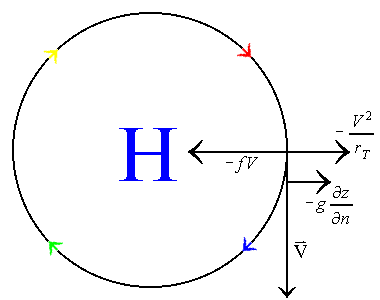 |
In the cases of the normal high and normal low, the flow is baric, meaning that the coriolis force and the pressure gradient force are in opposite directions of one another. The same is true for the anomalous high pressure system. However, the flow around the anomalous low pressure system is anti-baric and anti-cyclonic. Because of these types of flow around the anomalous low pressure system, the geostrophic velocity is in the opposite direction of the gradient wind velocity. Hence, the anomalous low pressure system is not much of a reality.
When comparing gradient wind speeds with geostrophic wind speeds for the same pressure gradient force, there are some differences. Gradient flow around a high pressure system will be faster than the geostrophic flow if the pressure gradient force is constant. The opposite is true when considering low pressure systems. In this case, the gradient wind around the low pressure system is less than the geostrophic wind if the pressure gradient force is constant. The formula below defines a ratio of geostrophic flow to gradient flow:
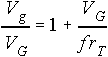
where:

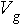 = Geostrophic wind speed
= Geostrophic wind speed

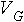 = Gradient wind speed
= Gradient wind speed
Thus, if the value of the ratio is greater than one, then the flow is cyclonic. If the value is less than one, the flow is anti-cyclonic.
 Next topic: Inertial flow
Next topic: Inertial flow
 Previous topic: Geostrophic flow
Previous topic: Geostrophic flow