|
|
|
The June distribution of the maximum wind speed, associated with each convective period in 5 kt
increments, also resulted in a peak in the 25-29 kt range. However, the drop off at higher wind speeds
is not nearly as pronounced as it was in May. The Gumbel curve maximum is in the upper 20's, similar
to May, but probabilities are higher for warning-level winds. In fact, June has the highest probabilities
of any of the warm season months for warning level events.
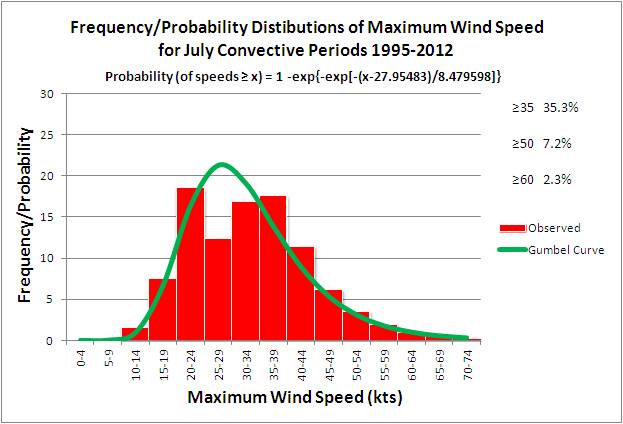
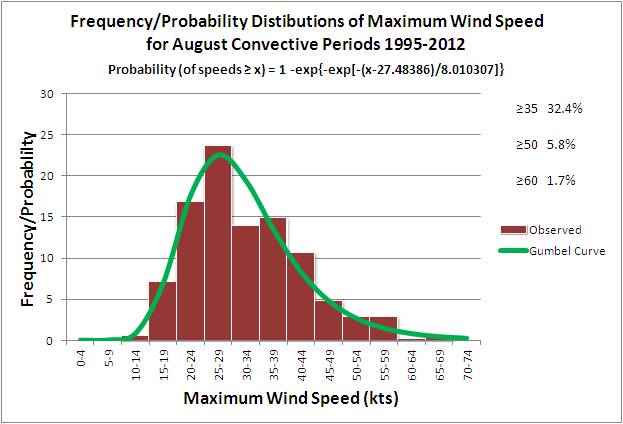
The probability of meeting or exceeding any speed threshold, given that convective winds occur, can be
found by integrating the Gumbel curve from that speed threshold to infinity. This can be done can be
done mathematically by using the equation shown in Figure 15b and plugging in a threshold value for x
(in kt). Setting x equal to the threshold values of 35, 50, and 60 kt, yields the probability
values shown in Figure 15b.
|